EXPLORANDO A INTERDISCIPLINARIDADE ENTRE MATEMÁTICA E CIÊNCIA DE ALIMENTOS UMA PROPOSTA DE ENSINO

Explorando a interdisciplinaridade entre matemática e ciência de alimentos uma proposta de ensino

Introdução

O estudo da equação do 1º grau, ou mais especificamente da equação linear, é de extrema importância, por ser a base para o estudo das funções (COELHO DA SILVA et al., 2015). Por uma outra perspectiva, o estudo desse tipo de equação possibilita que se faça associação entre a interpretação gramatical e a linguagem matemática com possibilidade de compreensão do sistema lógico envolvido. É possível ir além da identificação do que deve ser resolvido, dando oportunidade de construir o raciocínio matemático para tal ação (ALVES; DE MARCO, 2018).

Trabalhar o conteúdo matemático estabelecido para cada ano de formação é um grande desafio para os professores, considerando o interesse em querer construir o conceito com o propósito do estudante efetivamente compreender (LAGO; GOMES, 2019; LOPES, 2018). Metodologias que promovam o aprendizado calçado na realidade propiciam a redução do grau de dificuldade que envolve a matemática (Silva & Almeida, 2019).

O interesse em compreender o ensino e a aprendizagem da álgebra é recente (final dos anos 80 e início dos anos 90 do século passado) e a maior parte dos estudos realizados nesta temática conclui que o pensamento algébrico é o centro da aprendizagem do aluno (HILÁRIO et al., 2021). Na escola básica, as abordagens na álgebra se reduzem a “simplificar expressões algébricas, resolver equações e aprender regras para manipulação de símbolos”, e para uma mudança deste quadro é importante a generalização algébrica já ser proposta no ensino da aritmética (RODRIGUES; PINTO, 2020).

Considerando que a matemática tem papel essencial para o pensamento ordenado e criativo (COELHO; AGUIAR, 2018), não se pode apenas aplicá-la na resolução de problemas de forma automática e generalizada, sendo necessário compreender o problema para solucioná-lo, dando a oportunidade de desenvolver no estudante as competências e habilidades em raciocinar, argumentar e comunicar (Araújo et al., 2020).

Uma das dificuldades de aprendizado da matemática é a não percepção, ou interesse do aluno nas atividades utilizadas para a abordagem de um dado tema. Mesmo associada ao cotidiano, essa abordagem pode não surtir o efeito esperado no aprendizado, pois nem sempre está relacionada à vivência do aluno. Sendo assim, cabe ao professor promover experiências ricas e instigantes que propiciem um bom aprendizado (Cezario et al., 2020). Cabe ainda refletir quanto à formação do professor para lidar com conceitos novos durante a formação do aluno, abordando-os de forma diferenciada, cotidiana e lúdica. Estudo indica que a grande dificuldade de escrita, leitura e interpretação (As Dificuldades Do Ensino e Aprendizagem No Ensino Fundamental I, n.d.) é um fator de bloqueio no aprendizado matemático, e ciente desta realidade, é imprescindível que o professor de matemática lide com estas limitações, abordando o conteúdo visando o aprendizado tanto da matemática quanto no aperfeiçoamento associado a leitura e interpretação. Se o aluno não consegue ler e compreender o texto que envolve um problema, como conseguirá construir uma resolução?

            Considerando que o conhecimento das equações polinomiais é a base para a compreensão das funções polinomiais, Membros do National Council of Teachers of Mathematics (NCTM) indicaram como solução para minimizar a dificuldade apresentada pelas crianças (10 a 12 anos) na abordagem do conceito de funções, tanto do 1^o grau quanto do 2^o grau, promover a introdução de conceitos algébricos desde os primeiros anos escolares, adaptando a linguagem algébrica para o contexto da criança; essa proposta teve apoio de grande parte da comunidade de educadores matemáticos pelo mundo (Beck & Silva, 2019).

            Analisando o exposto, fica a questão: introduzir conceitos algébricos na infância facilitará ou prejudicará no aprendizado da matemática? É possível unir estes desafios e desenvolver atividades atrativas aos alunos e que alcancem o objetivo do ensino da temática proposta? Acredita-se que sim, e para tal está sendo apresentada propostas de atividades de ensino com a abordagem de conceitos indispensáveis para o bom aprendizado da equação do 1^o grau utilizando com base o conhecimento da composição dos macronutrientes em alimentos.

O processo de aprendizagem realizado de forma lúdica, relacionado com o conceito de brincar, favorece o desenvolvimento da linguagem, do raciocínio, da socialização, da iniciativa e da autoestima (MARRETI FELIX et al., 2021). Debater a saúde e a alimentação saudável no ambiente escolar é desejável. Sendo assim, adotar estratégias que integrem esta temática no projeto político pedagógico das escolas propiciará ações efetivas quanto ao binômio saúde x alimentação (PIASETZKI; BOFF, 2018). Mesmo não sendo mais praticada pelo atual guia alimentar, a pirâmide alimentar é bastante conhecida e ainda muito explorada em livros didáticos de ciências no ensino fundamental (COSTA; VINCHA; CARNEIRO, 2021), tornando-se muito útil nas atividades lúdicas desenvolvidas neste nível de formação educacional (REIS; SANTOS REINALDO, 2020) e, também, na análise da rotulagem nutricional (LOPES; CARVALHO; MACHADO, 2022). A proposta de um guia alimentar é promover a educação nutricional, sendo uma ferramenta clara e de fácil compreensão. Os guias alimentares na forma de pirâmide proporcionam maior percepção da variedade e proporcionalidade entre os grupos de alimentos, que são estabelecidos pelas características similares quanto a composição de nutrientes (Pereira et al., 2021).  

O conceito de equação do 1° grau será explorado, a partir do conhecimento básico dos alimentos e seus nutrientes. O conteúdo, englobando igualdade, proporcionalidade, porcentagem e equação do 1º grau, está subdividido em 4 aulas que irão consolidar conceitos fundamentais para a resolução das equações do 1° grau, bem como viabilizar à introdução deste conteúdo.

Metodologia

            Estarão sendo abordados os temas igualdade, proporcionalidade, porcentagem e equações do 1º grau em quatro aulas, também sendo exploradas as temáticas associadas a micronutrientes, composição dos alimentos, tipos de carboidratos e análise da rotulagem nutricional.

Explorando igualdade e proporcionalidade a partir da percepção sensorial da melancia e do melão

            Nesta primeira aula, os conceitos igualdade e proporcionalidade estarão sendo revistos a partir da dinâmica que envolve explorar o conteúdo de água da melancia e do melão, a partir da percepção sensorial. A BNCC estabelece que a compreensão da ideia de igualdade objetiva escrever diferentes sentenças de adições ou de subtrações de dois números naturais que resultem na mesma soma ou diferença (EF03MA11) e ainda que a resolução de problemas que envolvam variação de proporcionalidade direta entre duas grandezas, permita associar a quantidade de um produto ao valor a pagar, alterar as quantidades de ingredientes de receitas, ampliar ou reduzir escala em mapas, entre outros  (EF05MA12) (“Base Nacional Comum Curricular - Educação é a Base”, [s.d.]).

            Para o desenvolvimento da aula, sugere-se o seguinte material: a) fatias de melancia e fatias de melão; b) sendo possível, ferramentas computacionais para construção gráfica, por exemplo geogebra ou excel; c) prato fundo; d) garfos; copos e guardanapos.

Roteiro proposto:

O professor inicia a aula com a pergunta: qual fruta tem mais água: melancia ou melão? 

As respostas são anotadas no quadro, utilizando uma tabela com 2 colunas (melancia e melão) indicando o quantitativo de respostas de cada fruta.

Em seguida, o professor oferece a cada aluno um pequeno pedaço de melancia e pede que eles comam (é importante o pedaço de melancia seja cortado na hora, a partir de uma fatia que esteja com a casca). Na sequência, visando não haver influência no paladar, pede-se aos alunos que bebam um pouco de água (CUNHA; SILVA; SANDRI, 2018) e se oferece um pedaço de melão sem casca (também recém cortado). Após esta etapa, volta a perguntar: qual fruta tem mais água: melancia ou melão? Faz nova anotação no quadro utilizando uma tabela com 2 colunas (melancia e melão) indicando o quantitativo de respostas de cada fruta. Na sequência, o professor explora graficamente os resultados.

Em seguida o professor pega uma fatia grande de melancia com casa e retira a casca, fraciona a fruta e coloca no prato fundo descartável, enquanto os alunos observam. Faz o mesmo procedimento para o melão. Trabalha nas sequências a seguir, enquanto as frutas ficam no recipiente.

Questionando sobre a composição dos alimentos: o que tem nesses alimentos? Indica a composição de nutrientes, apresentando os macronutrientes: carboidratos, proteínas e lipídios (gorduras) e ainda a fração representada pela água (“TACO”, [s.d.])

Conhecendo os nutrientes dos alimentos explorando porcentagem e proporcionalidade

            Esta aula explora mais detalhadamente a interdisciplinaridade da matemática com a ciência de alimentos. Assim, está sendo apresentada proposta que irá explorar a composição dos macronutrientes e da água, na melancia e no melão, os diferentes grupos de carboidratos, permitindo explicar o comportamento da água nestas diferentes frutas e, ainda, a relação de calorias produzidas pelos nutrientes. Tal conteúdo pode ser aplicado para desenvolver as habilidades EF05MA12, EF06MA13 e EF07MA15 da BNCC (“Base Nacional Comum Curricular - Educação é a Base”, [s.d.]).

Roteiro proposto:

            A aula inicia com a apresentação da composição de água e outros nutrientes da melancia e do melão (figura 3) e a partir desta se destrincha a fração “outros nutrientes”, representando os macronutrientes: carboidratos, proteínas e lipídeos. Assim, são construídos novos gráficos de pizza a partir dos dados da tabela 1. Sugere-se utilizar as ferramentas geogebra ou excel e permitir que os alunos construam os gráficos referentes à composição centesimal da melancia e do melão.

Tabela 1 – Composição centesimal do melão e da melancia

Fonte - (“TACO”, [s.d.])

Explorando os gráficos construídos, onde será observado que a fração de carboidratos e a da água são as predominantes, o professor relaciona a liberação da água da melancia e a não liberação da água do melão à interação da água com a fração de carboidratos, apresentando os diferentes tipos destes: simples e complexo (figura 1)

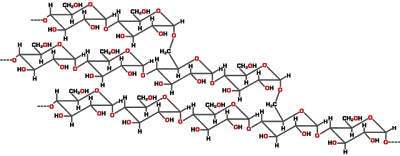
                                                                                           SACAROSE                                                                                              ESTRUTURA MOLECULAR PARCIAL DO AMIDO

                                                                                      Figura 1 – Estrutura molecular de um carboidrato simples (sacarose) e de um complexo (amido)

ESTRUTURA MOLECULAR PARCIAL DO AMIDO

Explorando equações polinomiais do 1º grau a partir da comparação da composição nutricional de porções de alimentos

            Nesta etapa, que pode ser dividida em duas aulas, a proposta é aproveitar combinações de alimentos para desenvolver as habilidades EF07MA18 e EF07MA15) (“Base Nacional Comum Curricular - Educação é a Base”, [s.d.]). Assim, a partir de uma mistura clássica, arroz e feijão, será desenvolvida uma equação geral para o cálculo de valor calórico. O teor de macronutrientes destes produtos está representado na tabela 2.

Tabela 2 – Teor de macronutrientes de 1 porção de arroz e feijão

Fonte - (“TACO”, [s.d.])

Também indica-se explorar, em aula específica,  a partir de diferentes opções de produtos variados, será proposto que o aluno defina os alimentos para uma refeição e, estabelecendo o valor calórico total da refeição, analise a proporção de gordura, considerando a recomendação de no máximo 30% de gorduras da ingestão total de calorias (“Alimentação saudável - OPAS/OMS | Organização Pan-Americana da Saúde”, [s.d.]).

Resultados e discussão

Explorando igualdade e proporcionalidade a partir da percepção sensorial da melancia e do melão

            O conceito de igualdade estará sendo explorado graficamente a partir das respostas dos alunos quanto a questão do conteúdo de água das frutas melancia e melão, minimizando a pouca atenção que é dada na construção de gráficos e interpretação dos mesmos durante a formação básica (Lima & Selva, 2020). É possível ao professor explorar o quantitativo de alunos que informaram melancia e melão antes e após o consumo das frutas e construir um gráfico em barras (formato sugerido) (figura 2).

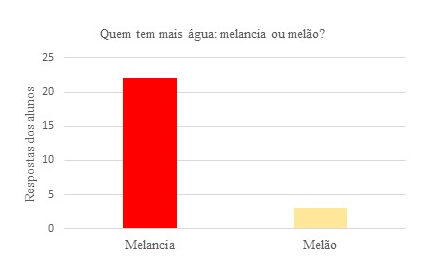
Figura 2 – Gráfico (podendo ser de diferentes formatos) explorando a questão “Quem tem mais água: melancia ou melão?” (turma hipotética com 25 alunos)

Explorando a composição dos alimentos (água e demais macronutrientes: proteínas, carboidratos e lipídeos), utilizando gráfico no formato de pizza; promove-se a oportunidade dos estudantes interpretarem um novo formato, estabelecendo o alimento que apresenta maior conteúdo de um nutriente específico, por exemplo, a água (alimentos A e D) e os carboidratos (alimentos B e C) (figura 3).

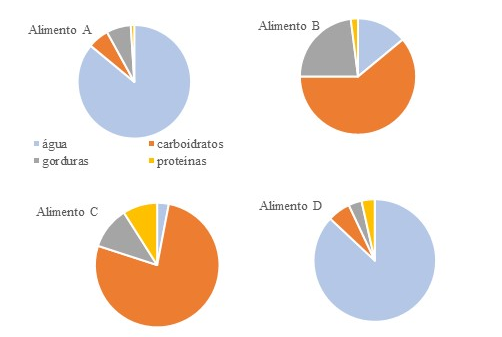
Figura 3 - Explorando a composição dos alimentos e a percepção visual dos que possuem maior quantidade de água e carboidratos (alimento A – polpa de abacate; alimento B – feijão preto; alimento C – biscoito doce; alimento D – leite integral) (“TACO”, [s.d.])

Tendo sido compreendido pelos alunos como interpretar um gráfico, o professor retorna ao recipiente que está com os pedaços de melancia e melão. Pela composição destas frutas, será possível perceber que a melancia “libera água” e o melão não. Certamente que ao constatar tal fato, os alunos serão induzidos a responder “melancia” quando questionados: “Qual fruta tem mais água: melancia ou melão?”. É feita a representação gráfica da composição nutricional destas frutas, explorando a fração água e o conjunto dos macronutrientes (carboidratos, proteínas e lipídeos) (figura 4 e tabela 3).

Figura 4 - Teor de água e outros nutrientes (somatório dos conteúdos de carboidratos, proteínas e lipídeos) no melão e na melancia (“TACO”, [s.d.])

Tabela 3 – Quantidades em gramas de água e outros nutrientes (carboidratos, proteínas e lipídeos) para 100g de melão e 100g de melancia

Fonte - (“TACO”, [s.d.])

Importante o professor explorar a figura 3, antes de apresentar os valores numéricos que representam as frações de água e outros nutrientes das frutas, para que os alunos percebam, que ambas as frutas apresentam as mesmas quantidades destas frações.

Sugere-se, apenas com a representação gráfica, que o professor proponha a seguinte atividade: Maria comeu 1 fatia de melancia (60g) e João comeu 1 fatia de melão (40g), quem ingeriu maior quantidade de água, João ou Maria? Na percepção dos autores, tal atividade promoverá uma leitura gráfica específica com as limitações do gráfico de pizza, quando não apresentados os valores das frações. Na sequência, para que o aluno desenvolva a atividade, é apresentada a tabela 3. Certamente que os dados desta irão propiciar desconfiança, considerando que é “visível” a água na melancia e não no melão. 

E assim, cria-se uma oportunidade para que o aluno conheça um pouco mais sobre a composição dos alimentos e permite que o professor proponha atividade complementar, promovendo uma conexão para a sequência das aulas, questionando: “Tendo igual quantidade de água na melancia e no melão, por que a água não aparece no recipiente que contém o melão?”.  

Conhecendo os nutrientes dos alimentos explorando porcentagem e proporcionalidade

A partir dos dados da tabela 3 é feita a representação gráfica da composição centesimal da melancia e do melão (figura 5). 

Figura 5 – Macronutrientes (g/100g) em melão e melancia (“TACO”, [s.d.])

A partir dos dados da tabela 1, é possível trabalhar diferentes resoluções para explorar a quantidade de carboidratos no consumo de 1 fatia de melão (115g) e de 1 fatia de melancia (148g), sendo proposta:

                        Melancia                             Melão

100g           8,3g carboidratos               8,1g carboidratos

50g       4,15% carboidratos              4,05% carboidratos

10g             0,83g carboidrato            0,81g carboidrato

5g             0,415g carboidrato          0,405g carboidrato

1g             0,083g carboidrato           0,081g carboidrato

1 fatia de melão (115g) tem 8,1 + 0,81 + 0,405 de carboidratos

1 fatia de melão (115g) tem 9,315g de carboidratos

115g de melão = 9,315g de carboidratos

1 fatia de melancia (148g) tem   de carboidratos

1 fatia de melancia (148g) tem 12,284g de carboidratos

148g de melancia = 12,284g de carboidratos

            Para responder a questão quanto a razão da água da melancia ser perceptível e a do melão não, é importante o professor observar se todos os alunos perceberam que a quantidade de carboidratos nas diferentes frutas é muito similar e, então, explorar se a pequena diferença entre eles é justificativa para tal fato. Com esta reflexão, o professor informa que não se conhece um alimento apenas pela quantidade dos macronutrientes, mas que cada macronutriente apresenta diferentes características e assim, explora os carboidratos simples e complexos, indicando os grupamentos polares e sua capacidade de interação com a água, onde os carboidratos complexos “prendem” a água (FREITAS; GONÇALVES, 2020). Dessa forma, o professor estimula os alunos a concluírem que o melão apresenta carboidratos complexos com maior capacidade de “prender” a água do que a melancia.

            Em seguida o professor deve explorar o conceito da alimentação como fornecedor de energia, indicando a quantidade de calorias produzida por cada nutriente, a saber: 1 g de carboidrato produz 4 quilocalorias de energia, 1g de proteína produz 4 quilocalorias de energia e 1g de lipídeos produz 9 quilocalorias de energia. Sugere-se trabalhar com as seguintes questões visando desenvolver as habilidades EF05MA12, EF06MA13 e EF07MA15 (“Base Nacional Comum Curricular - Educação é a Base”, [s.d.]):

1. João comeu 1 pedaço de melancia (60g). Maria comeu 1 pedaço de melão (50g). 

a) Quanta energia foi produzida pelo consumo das proteínas presentes nessas porções dessas frutas?

b) Quanta energia foi produzida pelo consumo dos carboidratos presentes nesss porções dessas frutas?

c) Quem produziu mais energia a partir dessas frutas: João ou Maria?

Solução proposta a partir dos dados da tabela 1:

                                     Melancia                         Melão

100g                       0,9g proteína                   0,7g proteína

  50g                      0,45g proteína                 0,35g proteína

  10g                      0,09g proteína                 0,09g proteína

100g                    8,1g carboidratos               8,3g carboidratos

  50g                    4,05g carboidratos              4,15g carboidratos

  10g                      0,81g carboidrato               0,83g carboidrato

1g proteínas/          4 quilocalorias                      4 quilocalorias

   carboidratos

0,5g proteínas/        2 quilocalorias                     2 quilocalorias

   carboidratos

0,1g proteínas/        0,4 quilocaloria                  0,4 quilocaloria

   carboidratos

0,01g proteínas/      0,04 quilocaloria                  0,04 quilocaloria    

  carboidratos

a)      60g de melancia têm 0,45 + 0,09g de proteína = 0,54g de proteína

         0,54g de proteína produz 2 + (4 x 0,04) = 2,16 quilocalorias

         50g de melão têm 0,35g de proteína

         0,35g de proteína produz (3 x 0,4) + (5 x 0,04) = 1,4 quilocaloria

b)      60g de melancia têm 4,05 + 0,51g de carboidratos = 4,56g de carboidratos

       4,56g de carboidratos produz (4 x 4) + 2 + (6 x 0,04) = 18,24 quilocalorias

          50g de melão têm 4,15g carboidratos

       4,15g de carboidratos produzem (4 x 4) + 0,04 + (5 x 0,04) = 16,6 quilocalorias

c)      Quantidade de energia produzida por 60g de melancia –> 2,16 + 18,24 = 20,4 quilocalorias

         Quantidade de energia produzida por 57g de melão –> 1,4 + 16,6 = 18 quilocalorias

        João obteve mais energia do que Maria

Visando incentivar a percepção quanto a diferença calórica de produtos similares, sugere-se explorar rótulos de produtos, conforme roteiro a seguir:

a)      Preenchimento de tabela (modelo tabela 4) com no mínimo dois produtos similares, por exemplo, biscoito recheado de diferentes marcas

Tabela 4 – Modelo de tabela com informações de rótulos

b)      Estimar quantidades de consumo dos produtos com base nas porções e apresentar questões que explorem o consumo associado à fração de carboidratos e ao teor calórico, bem como analisar o valor calórico informado no rótulo a partir da determinação do cálculo do teor calórico.

Exemplo a partir dos dados de duas marcas comerciais, A e B:

 I)                   Calcule o valor calórico de uma porção de cada produto e observe se é igual ao que está sendo informado no rótulo

Proposta de resolução

4 kcal – produzidas por 1g de proteína e por 1g de carboidratos

9 kcal – produzidas por 1 g de lipídeos (gorduras totais)

Marca A – valor calórico = (22 x 4) + (1,8 x 4) + (4,8 x 9)

                   valor calórico = 138,4 kcal // informação de rótulo 137 kcal

Marca B – valor calórico = (21 x 4) + (1,6 x 4) + (6,1 x 9)

                   valor calórico = 145,3cal // informação rótulo 143

II)                João comeu 4 biscoitos da marca A e Maria 5 biscoitos da marca B. Quem consumiu mais carboidratos, também foi quem consumiu mais calorias? Quem consumiu mais calorias, foi quem consumiu maior quantidade de biscoitos?

Proposta resolução

                                                   Marca A 

2 unidades (1 porção)          22g de carboidratos

                                            138,4 calorias (calculado anteriormente)

1 unidade                            11g de carboidratos

                                            69,2 calorias

4 unidades =  22 x 2 = 44g carboidratos

4 unidades =  138,4 x 2 = 276,8 calorias

                                                 Marca B 

3 unidades (1 porção)          21g de carboidratos

                                            131,8 calorias (calculado anteriormente)

1 unidade                              7g de carboidratos

                                            43,93 calorias

5 unidades = 7 x 5 = 35g de carboidratos

5 unidades = (43,93 x 5) = 219,65 calorias

João consumiu mais carboidratos e calorias e Maria consumiu maior quantidade de biscoitos

Explorando as equações polinomiais do 1º grau a partir da comparação da composição nutricional de porções de alimentos

            Com os dados da tabela 2 e sabendo que 4 quilocalorias são produzidas por 1g de carboidratos e 1 g de proteínas e, ainda, que 9 quilocalorias são produzidas por 1 g de lipídeo, o professor lança desafio para que se estabeleça uma solução geral para o cálculo do valor calórico, que pode ser aplicada a cada produto e a combinação do arroz e feijão.

Proposta de resolução

Valor calórico do arroz

1g de proteína produz 4 quilocalorias; 1g de carboidratos produz 4 quilocalorias; 1g de gordura produz 9 quilocalorias

Valor calórico = 4 * massa de proteínas  +  4 * massa de carboidratos  +  9 * massa de gordura

Valor calórico = 4 (massa de proteínas  +  massa de carboidratos)  +  9 * massa de gordura

Valor calórico de 6 colheres de sopa de arroz + 19 colheres de sopa de feijão = ?

Valor calórico = 4 * (2,6 + 4,5 + 28,2 + 14) + 9 * (0,4 + 0,5)

Valor calórico = 4 * (49,3) + 9 * (0,9)

Valor calórico =  197,2 + 8,1           Valor calórico = 205,3 kcal

            A alimentação envolve um complexo sistema de interações humanas e, assim, a escolha alimentar não pode ser apenas associada às características nutricionais (OTTO; RIBEIRO, 2020). Ela também deve promover o empoderamento para escolhas alimentares saudáveis, perpassando pela conscientização de temas associados à saúde e aos cuidados com a alimentação (VINCHA et al., 2021). Aproveitar uma aula de matemática para explorar escolhas alimentares é uma forma de promover o cuidado com a saúde, bem como ampliar a percepção da ciência da matemática no cotidiano.

            A tabela 5 apresenta opções para estabelecer uma refeição. A partir desta, o professor pode explorar as questões associadas à escolha alimentar, conforme exemplo a seguir:

            Está sendo permitido que você escolha o que quer comer no almoço. Após ter definido sua(s) preferência(s) e quantidades, calcule o valor calórico da refeição.

Proposta de resolução.

Refeição 1 – 8 colheres de sopa de arroz

                    24 colheres de sopa de feijão

                      4 colheres de sopa de salada de vegetais crus com azeite de oliva e com sal

                      2 empadas de frango

Refeição 2 – 2 unidades de sanduíche, cachorro quente, (com pão para hot dog e salsicha de frango), com ketchup, mostarda, maionese, milho, ervilha, purê de batata, molho vinagrete e batata palha

Refeição 3 – 8 colheres de sopa de salada, batata com maionese

                     4 unidades de salsicha tradicional com molhe de tomate

                     6 colheres de sopa arroz

                   10 colheres de sopa feijão

Valor calórico = 4 * massa de proteínas  +  4 * massa de carboidratos  +  9 * massa de gordura

Valor calórico refeição 1

Total proteínas (g)= (8 * 0,42) + (24 * 0,24) + (4 * 0,11) + (2 * 6,9) = 23,36

Total lipídeos  (g ) =  (8 * 0,07) + (24 * 0,03) + (4 * 1,1 ) +  (2 * 15,6 ) = 36,88

Total carboidratos (g)  = (8 * 4,5 ) +  (24 * 0,74 ) +  (4 * 1,2) + (2 * 47,5) = 153,56

Valor calórico = 4 (23,36 + 153,56)  + 9 * 36,88 = 1039,6 kcal

Valor calórico refeição 2

Total proteínas (g)= 17,8 * 2 = 53,6

Total lipídeos  (g ) =  25,1 * 2 = 50,2

Total carboidratos (g) =  70,5 * 2 = 141

Valor calórico = 4 (35,6 + 141)  + 9 * 50,2 = 1158,2 kcal

Valor calórico refeição 3

Total proteínas (g)= (8 * 0,18) + (2 * 11,4) + (6 * 0,42) + (10 * 0,24) = 29,16

Total lipídeos  (g ) =  (8 * 3,1) + (2 * 16,5) + (6 * 0,07) +  (10 * 0,03 ) = 58,52

Total carboidratos (g) = ( 8 * 2) + (2 * 7,84) + (9 * 4,5) + (10 * 0,74) = 66,08

Valor calórico = 4 (29,16 + 58,52)  + 9 * 66,08 = 907,64 kcal

Visando uma reflexão sobre a escolha do aluno, é proposta uma análise quanto à adequação do teor % de lipídeos da refeição, considerando a recomendação de no máximo 30% de gorduras da ingestão total de calorias (“Alimentação saudável - OPAS/OMS | Organização Pan-Americana da Saúde”, [s.d.]).

Proposta de resolução

Refeição 1 

Valor calórico total = 1039,6kcal

                     Energia produzida por lipídeos = 36,88 * 9 = 331,92  kcal

                     30% do valor calórico total = 0,3 * 1039,6 = 311,88 kcal

                     % valor calórico real = (331,92 / 1039,6) * 100 = 31,93%

Refeição 2 

Valor calórico total = 1158,2kcal

                     Energia produzida por lipídeos =50,2 * 9 = 451,8  kcal

                     30% do valor calórico total = 0,3 * 1158,2  = 347,46 kcal

                     % valor calórico real = (451,8 / 1158,2) * 100 = 39,0%

Refeição 3 

Valor calórico total = 907,64 kcal

                     Energia produzida por lipídeos = 58,52 * 9 = 526,6892  kcal

                     30% do valor calórico total = 0,3 * 907,64 = 277,29 kcal

                     % valor calórico real = (526,68 / 907,64) * 100 = 58,0%

As refeições apresentadas como exemplo são possibilidades reais de escolhas alimentares e, conforme observado, nenhuma destas se adequa ao que se recomenda quanto o teor de gorduras. Certamente é importante ressaltar que tal recomendação de no máximo 30% de gordura na alimentação, considera o consumo diário e não específico em uma alimentação.

Acredita-se que com esta análise, além do educador trabalhar diferentes habilidades matemáticas, ele possa exercer papel amplo na formação da criança, dialogando ainda com as atividades desenvolvidas a partir do Programa de Saúde na Escola, que também proporciona ações visando promulgar a alimentação saudável (MALDONADO et al., 2022).

Tabela 5 – Teor de macronutrientes em diferentes produtos

Fonte - (TACO, n.d.; Tabela Brasileira de Composição de Alimentos - USP, n.d.)

Considerações finais

            Existem alguns desafios para que a formação de um cidadão, entendendo que esta engloba educação, saúde e cultura, em nosso país seja realmente considerada satisfatória. Dois destes desafios, o aprendizado da matemática e a alimentação saudável, foram explorados de forma conjunta, lúdica e com a pretensão de semear o interesse no conhecimento do alimento, permitindo escolhas conscientes. A intenção é desmistificar conceitos básicos da ciência da matemática, incorporando no cotidiano, outros exemplos além dos tradicionalmente explorados nas diferentes referências e livros didáticos.

            A proposta apresentada indica um dos muitos caminhos que podem ser utilizados na relação da educação nutricional com a matemática. Acredita-se que tal caminho, com o interesse nato na alimentação, pode aguçar a curiosidade e o interesse dos alunos em ambas as áreas, ciência de alimentos e ciência dos números e operações numéricas.

Agradecimento – os autores agradecem o incentivo a esta produção, a partir de atividade didática desenvolvida na disciplina álgebra para educação básica, sob a responsabilidade da Profa. Dra. Aline Caetano Bernardes da Silva, do curso de graduação em licenciatura em matemática.

Referências bibliográficas

Alimentação saudável - OPAS/OMS | Organização Pan-Americana da Saúde. Disponível em: <https://www.paho.org/pt/topicos/alimentacao-saudavel>. Acesso em: 5 set. 2022.

ALVES, B. A. S.; DE MARCO, F. F. Equações de 1° grau e estratégias para sua resolução por estudantes do 7° ano do ensino fundamental. Obutchénie (Online), p. 113–138, 2018.

ARAÚJO, H. C. DE; FEITOSA, S. DE A. ;; MENDOZA, H. J. G. View of Diagnosis of the level of learning through the Activity Situation Problem Student in the third year for Elementary School students of the College of Application. Research, Society and Development, v. 9, n. 7, p. e44973686, 2020.

Base Nacional Comum Curricular - Educação é a Base. Disponível em: <http://basenacionalcomum.mec.gov.br/abase/#estrutura>. Acesso em: 14 ago. 2022.

CEZARIO, A. DA S. O. et al. Evaluation of the use of mathematical knowledge in the daily lives of high school students in Cajazeirinhas/PB. Research, Society and Development, v. 9, n. 8, p. e371985732, jul. 2020.

COELHO DA SILVA, I. et al. Estudando equação do 1o grau por meio do uso de fontes históricas: o papiro de Rhind. Boletim Cearense de Educação e História da Matemática, v. 2, n. 6, p. 37–48, 31 maio 2015.

COELHO, F. U.; AGUIAR, M. A história da álgebra e o pensamento algébrico: correlações com o ensino. Estudos Avançados, v. 32, n. 94, p. 171–187, 2018.

COSTA, G. B.; VINCHA, K. R. R.; CARNEIRO, A. C. L. L. Abordagem do Guia Alimentar para a População Brasileira em livros de ciências do ensino fundamental. Demetra: Alimentação, Nutrição e Saúde, v. 16, p. e51578–e51578, 2021.

CUNHA, A. H. N.; SILVA, S. M. DA C. E; SANDRI, D. Análise sensorial de tomates Sweet Grape em diferentes condições de armazenamento. Multi-Science Journal, v. 1, n. 4, p. 39–43, 2018.

FREITAS, S. M.; GONÇALVES, É. C. B. DE. Carboidratos - interação com a água. , 5 ago. 2020. Disponível em: <http://educapes.capes.gov.br/handle/capes/715458>. Acesso em: 3 set. 2022

HILÁRIO, C. et al. Pensamento Algébrico na aprendizagem de equações do 1^o grau. Revista Eletrônica de Educação Matemática, v. 16, p. 1–18, 2021.

LAGO, A. S.; GOMES, L. P. S. Resolução de problemas e o ensino de sistemas de equações do 1o grau: reflexões de um grupo de Professores de Matemática. Revista Interfaces da Educação, v. 10, n. 28, p. 144–167, 2019.

LIMA, I. B.; SELVA, A. C. V. Construção de gráficos de barras no Ensino Fundamental da Educação de Jovens e Adultos. Jornal Internacional de estudos em educação matemática, v. 13, n. 2, p. 162, 2020.

LOPES, J. F.; CARVALHO, M. DE A.; MACHADO, N. C. Rotulagem de alérgenos alimentares em alimentos embalados segundo grupos alimentares da pirâmide brasileira: análise da descrição, riscos e ambiguidades. Revista paulista de pediatria, v. 40, 2022.

LOPES, T. B. Ensino de falsas operações matemáticas como agente dificultador na aprendizagem de equações do 1^o grau. Revista Cocar, v. 12, n. 23, p. 10–33, 2018.

MALDONADO, L. et al. Proposta de educação alimentar e nutricional integrada ao currículo de Educação Infantil e Ensino Fundamental. Cadernos de saúde pública, v. 37, n. suppl 1, 2022.

MARRETI FELIX, A. et al. Qualitative Analysis of the “Healthy Growing at School Program” - Vision of Health Professionals, School Community and Family. Journal of Human Growth and Development, v. 31, n. 1, p. 76–83, 28 abr. 2021.

OTTO, A. F. N.; RIBEIRO, M. A. A escolha alimentar e a complexidade dos sistemas humanos. Revista Brasileira de Psicoterapia, v. 22, n. 1, 2020.

PEREIRA, J. Q.; SANTOS, B. C.; LIMA, D. C. DE. Desenvolvimento de uma pirâmide alimentar adaptada à população vegetariana brasileira. Revista Segurança Alimentar e Nutricional (Online), v. 28, p. e021023, 2021.

PIASETZKI, C. T. DA R.; BOFF, E. T. DE O. Educação Alimentar E Nutricional E a Formação De Hábitos Alimentares Na Infância. Revista Contexto & Educação, v. 33, n. 106, p. 318, 2018.

REIS, W. A. DOS; SANTOS REINALDO, A. M. DOS. Estratégias de Educação Alimentar e Nutricional no ambiente escolar: uma revisão integrativa. Revista de atenção primária saúde, v. 21, n. 4, 2020.

RODRIGUES, M. DA S. C.; PINTO, M. M. F. Caracterizações do Pensamento Algébrico na Escola Básica. Abakós, v. 8, n. 1, p. 86–102, 2020.

SILVA, N. R. DA; ALMEIDA, J. J. P. DE. Mathematical modeling: a methodological alternative for basic education. Research, Society and Development, v. 8, n. 3, p. e4083805, jan. 2019.

Tabela Brasileira de Composição de Alimentos - USP. Disponível em: <http://www.intranet.fcf.usp.br/tabela/resultado.asp?IDLetter=C&IDNumber=579>. Acesso em: 14 jun. 2022.

TACO. Disponível em: <https://www.nepa.unicamp.br/taco/tabela.php?ativo=tabela>. Acesso em: 2 set. 2022.

VINCHA, K. R. R. et al. Identificando elementos de empoderamento e autonomia nas escolhas alimentares em grupos de Educação Alimentar e Nutricional: uma pesquisa qualitativa. Demetra: Alimentação, Nutrição e Saúde, v. 16, p. e49454–e49454, 2021.