BRINCANDO, CONHECENDO OS ALIMENTOS E CONSTRUINDO O PENSAMENTO LÓGICO
INTRODUÇÃO
O interesse em compreender o ensino e a aprendizagem da álgebra é recente (final dos anos 80 e início dos anos 90 do século passado) e a maior parte dos estudos realizados nesta temática conclui que o pensamento algébrico é o centro da aprendizagem do aluno (HILÁRIO et al., 2021). Na escola básica, as abordagens na álgebra se reduzem a “simplificar expressões algébricas, resolver equações e aprender regras para manipulação de símbolos”, e para uma mudança deste quadro é importante a generalização algébrica já ser proposta no ensino da aritmética (RODRIGUES; PINTO, 2020).
Considerando que a matemática tem papel essencial para o pensamento ordenado e criativo (COELHO; AGUIAR, 2018), não se pode apenas aplicá-la na resolução de problemas de forma automática e generalizada, sendo necessário compreender o problema para solucioná-lo, dando a oportunidade de desenvolver no estudante as competências e habilidades em raciocinar, argumentar e comunicar (Araújo et al., 2020). Uma das dificuldades de aprendizado da matemática é a não percepção, ou interesse do aluno nas atividades utilizadas para a abordagem de um dado tema. Mesmo associada ao cotidiano, essa abordagem pode não surtir o efeito esperado no aprendizado, pois nem sempre está relacionada à vivência do aluno. Sendo assim, cabe ao professor promover experiências ricas e instigantes que propiciem um bom aprendizado (Cezario et al., 2020).
Sabendo que o conhecimento das equações polinomiais é a base para a compreensão das funções polinomiais, Membros do National Council of Teachers of Mathematics (NCTM) indicaram como solução para minimizar a dificuldade apresentada pelas crianças (10 a 12 anos) na abordagem do conceito de funções, tanto do 1o grau quanto do 2o grau, promover a introdução de conceitos algébricos desde os primeiros anos escolares, adaptando a linguagem algébrica para o contexto da criança; essa proposta teve apoio de grande parte da comunidade de educadores matemáticos pelo mundo (Beck & Silva, 2019).
Analisando o exposto, fica a questão: introduzir conceitos algébricos na infância facilitará ou prejudicará no aprendizado da matemática? É possível unir estes desafios e desenvolver atividades atrativas aos alunos e que alcancem o objetivo do ensino da temática proposta? Acredita-se que sim.
O processo de aprendizagem realizado de forma lúdica, relacionado com o conceito de brincar, favorece o desenvolvimento da linguagem, do raciocínio, da socialização, da iniciativa e da autoestima (MARRETI FELIX et al., 2021). Debater a saúde e a alimentação saudável no ambiente escolar é desejável. Sendo assim, adotar estratégias que integrem esta temática no projeto político pedagógico das escolas propiciará ações efetivas quanto ao binômio saúde x alimentação (PIASETZKI; BOFF, 2018).
Mesmo não sendo mais praticada pelo atual guia alimentar, a pirâmide alimentar é bastante conhecida e ainda muito explorada em livros didáticos de ciências no ensino fundamental (COSTA; VINCHA; CARNEIRO, 2021), tornando-se muito útil nas atividades lúdicas desenvolvidas neste nível de formação educacional (REIS; SANTOS REINALDO, 2020).
O objetivo desta atividade é explorar as operações matemáticas e o conceito de igualdade aplicando a ciência dos alimentos promovendo a construção do raciocínio lógico.
Conhecendo a pirâmide alimentar com o foco na ciência dos alimentos
A pirâmide alimentar está sendo apresentada, indicando a construção da mesma com base nas proporções majoritárias dos macronutrientes e a divisão em grupos fontes de nutrientes e compostos bioativos. A finalidade principal desta etapa é proporcionar conhecimento básico sobre os grupos de alimentos, visando estabelecer os padrões a serem explorados nas atividades envolvendo o ensino da matemática. A pirâmide padrão que será utilizada está representada na figura 1
. 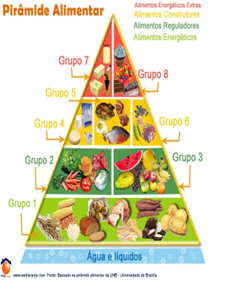
Figura 1 – Pirâmide alimentar
Fonte: (“Pirâmide Alimentar: grupos e atualização”, [s.d.])
2.2. Explorando a pirâmide alimentar e as operações matemáticas básicas
A partir das fontes de nutrientes (Tabela Brasileira de Composição de Alimentos - USP, n.d.) associadas a cada grupo dos alimentos, a saber: grupo 1 (carboidratos), grupo 2 (compostos bioativos) grupo 3 (compostos bioativos), grupo 4 (proteínas), grupo 5 (proteínas), grupo 6 (proteínas), grupo 7 (lipídeos) e grupo 8 (carboidratos), estarão sendo propostas as seguintes atividades:
I – Vovó Didira adora os seus netinhos e sabe que eles gostam muito de sorvete. Hoje ela vai preparar o sorvete para os seus netos. Ela prefere fazer, pois acredita que o sorvete comercial é colorido com corantes. Para ficar um colorido diferente ela usa uma variedade de frutas. As frutas são ricas em compostos bioativos que fazem muito bem para a saúde.
Para o preparo do sorvete, vovó Didira está usando 5 peras, 12 maçãs, 7 bananas e 3 abacaxis. Indique, por dois caminhos distintos, quantas frutas usará no preparo do sorvete.
Na resolução do problema, estará sendo relembrado o sistema de numeração para que, além da contagem, a solução do exercício seja construída, conscientemente, associada ao sistema de numeração, visando não criar apenas um algoritmo para a adição e sim, compreender como este é definido e deve estar sendo sempre relembrado em todas as fases da formação básica
II) Vovó Didira está no mercado e no carrinho de compras estão as frutas que separou para preparar sorvete para os seus netos: 5 peras, 12 maçãs, 7 bananas e 3 abacaxis. Ela acaba de receber uma ligação e fica sabendo que alguns netos não poderão vir visitá-la. Se ela retirar 1 pera, 5 maçãs, 4 bananas e 1 abacaxi do carrinho, quantas frutas irá levar? Resolva o problema indicando 2 formas distintas de solução.
Aqui, o sistema de contagem será utilizado como uma das formas de resolução e ainda, relembrando o conceito do “caminho inverso” da adição. A partir do sistema de numeração, o algoritmo será construído, visando aplicação dos conceitos de forma natural e não apenas criando uma regra de aplicação numérica.
III) O sorvete da vovó Didira é um sucesso. Sua sobrinha está fazendo 15 anos e pediu que vovó Didira preparasse sorvete para os seus convidados. Quando vovó Didira recebe seus 8 netinhos o sorvete que ela prepara com 5 peras, 12 maçãs, 7 bananas e 3 abacaxis é suficiente para todos. Sua sobrinha estará recebendo 40 convidados, quantas frutas serão compradas ao todo? Qual quantidade de cada fruta?
Indique a resolução aplicando duas formas distintas.
A proposta desta atividade é trabalhar o conceito de multiplicação aplicando o sistema de numeração, o sistema de contagem e a tabuada, na perspectiva da compreensão dos algoritmos e não apenas aplicação de uma regra e promover a memorização natural das tabuadas, a partir da fixação de seus conceitos e aplicabilidade prática
IV) Para o preparo de tanto sorvete, vovó Didira comprou uma máquina que corta as frutas em pedaços. A máquina funciona cortando apenas no meio o que é adicionado nela. Vovó Didira pegou uma maçã e colocou na máquina. Cada pedaço cortado, colocou novamente na máquina. Todos os pedaços de maçã foram colocados em uma tigela. Quantos pedaços de maçã vovó Didira colocou na tigela? Indique a resolução aplicando duas formas distintas.
A divisão será trabalhada a partir do conceito de fração. A percepção da operação inversa da multiplicação também será explorada, na perspectiva de compreensão dos algoritmos envolvidos nas diferentes operações básicas.
Na finalização da atividade, será feita uma reflexão quanto a prática de aplicar a prova real (operações inversas) em todas as operações matemáticas básicas.
2.3. Explorando os grupos de alimentos para trabalhar o conceito de igualdade
Trabalhar o conceito de igualdade não é algo tão simples, quando se pretende compreender a complexidade do tema (BARBOZA, PAZUCH, RIBEIRO, 2021; LUNA, MERLINI, FERREIRA, 2021). A percepção de equivalência, para uma compreensão do significado do termo, auxilia na construção do pensamento e posteriormente na aplicação matemática da propriedade. Assim, nesta fase a primeira atividade proposta será promover a percepção da equivalência dos alimentos de cada grupo associado ao nutriente majoritário.
Gerar associações entre os diferentes alimentos fontes de proteínas, compostos bioativos, carboidratos “bons” e carboidratos “guloseimas”, permitirá que a criança comece a perceber sua alimentação e a presença das fontes de todos os nutrientes em sua alimentação.
Para estabelecer relações de igualdade numérica, estará sendo apresentado o seguinte questionamento:
Vovó Didira prepara sua receita de sorvete utilizando 5 peras, 12 maçãs, 7 bananas e 3 abacaxis. Sua amiga Magali, utiliza no preparo de sua receita de sorvete 5 maçãs, 3 peras, 3 caquis, 6 uvas, 7 bananas e 3 abacaxis. No preparo das receitas, a quantidade total de frutas que a vovó Didira usa é a mesma que a Magali usa? Os sorvetes são iguais?
3. CONSIDERAÇÕES FINAIS
O aprendizado da matemática se dá progressivamente permitindo que cada questionamento possibilite um olhar diferenciado na identificação das relações matemáticas (OLIVEIRA; PAULO, 2021). Promover o desenvolvimento do pensamento lógico é conduzir o ensino da matemática de forma a não coibir as diversas possibilidades que a criança tem de perceber a lógica e as relações numéricas. Trabalhar os conceitos básicos e propiciar diferentes caminhos para solucionar problemas é um querer que todo profissional que atua na formação básica da criança deve ter. Ter a possibilidade, em paralelo à construção do pensamento lógico, associar o conhecimento da ciência dos alimentos é promover a saúde, conscientizando a prática da alimentação saudável.
REFERÊNCIAS
ARAÚJO, H. C. DE; FEITOSA, S. DE A. ; MENDOZA, H. J. G. View of Diagnosis of the level of learning through the Activity Situation Problem Student in the third year for Elementary School students of the College of Application. Research, Society and Development, v. 9, n. 7, p. e44973686, 2020.
BARBOZA, L. C. DE S.; PAZUCH, V.; RIBEIRO, A. J. Tarefas para a aprendizagem de professores que ensinam matemática nos anos iniciais. Zetetiké, v. 29, p. e021009, 2021.
CEZARIO, A. DA S. O. et al. Evaluation of the use of mathematical knowledge in the daily lives of high school students in Cajazeirinhas/PB. Research, Society and Development, v. 9, n. 8, p. e371985732, jul. 2020.
COELHO, F. U.; AGUIAR, M. A história da álgebra e o pensamento algébrico: correlações com o ensino. Estudos Avançados, v. 32, n. 94, p. 171–187, 2018.
COSTA, G. B.; VINCHA, K. R. R.; CARNEIRO, A. C. L. L. Abordagem do Guia Alimentar para a População Brasileira em livros de ciências do ensino fundamental. Demetra: Alimentação, Nutrição e Saúde, v. 16, p. e51578–e51578, 2021.
HILÁRIO, C. et al. Pensamento Algébrico na aprendizagem de equações do 1o grau. Revista Eletrônica de Educação Matemática, v. 16, p. 1–18, 2021.
LUNA, A. V. D. A.; MERLINI, V. L.; FERREIRA, Â. A. B. DO C. A igualdade na aula de Matemática da Educação Infantil: por que devemos ficar atentos ao usar esse sinal? Em Teia | Revista de Educação Matemática e Tecnológica Iberoamericana, v. 12, n. 3, 2021.
MARRETI FELIX, A. et al. Qualitative Analysis of the “Healthy Growing at School Program” - Vision of Health Professionals, School Community and Family. Journal of Human Growth and Development, v. 31, n. 1, p. 76–83, 28 abr. 2021.
OLIVEIRA, V. DE; PAULO, R. M. Pensamento algébrico nos anos iniciais: o que pensam os professores? Em Teia | Revista de Educação Matemática e Tecnológica Iberoamericana, v. 12, n. 3, 2021.
PIASETZKI, C. T. DA R.; BOFF, E. T. DE O. Educação Alimentar E Nutricional E a Formação De Hábitos Alimentares Na Infância. Revista Contexto & Educação, v. 33, n. 106, p. 318, 2018.
Pirâmide Alimentar: grupos e atualização . Disponível em: <https://www.todoestudo.com.br/biologia/piramide-alimentar>. Acesso em: 7 jul. 2023.
REIS, W. A. DOS; SANTOS REINALDO, A. M. DOS. Estratégias de Educação Alimentar e Nutricional no ambiente escolar: uma revisão integrativa. Revista de atenção primária saúde, v. 21, n. 4, 2020.
RODRIGUES, M. DA S. C.; PINTO, M. M. F. Caracterizações do Pensamento Algébrico na Escola Básica. Abakós, v. 8, n. 1, p. 86–102, 2020.
Tabela Brasileira de Composição de Alimentos - USP. Disponível em: <http://www.intranet.fcf.usp.br/tabela/resultado.asp?IDLetter=C&IDNumber=579>. Acesso em: 09 jul. 2023.